Types of solving equations:
- Factorisation
Example: y = x^2 + x - 6
Factorise by trial and error
You should get y = (x+3)(x+2)
-------------------------------------------------------------------------
However there is another type: what happens when x^2 + x -6 = 0
The method will be the same as the factorisation
Except that the equation will be shown as (x+3)(x-2) = 0
Therefore if this equation is equivalent to zero, either (x+3) = 0 or (x-2) = 0 as something-zero multiplied by something is zero.
Hence, x = -3 OR x = 2 because if x is 3, (x+3) is 0 and if x is 2, (x-2) = 0.
- General formula
y = -(b) ± √ (b)^2 - 4(a)(c) / 2(a)
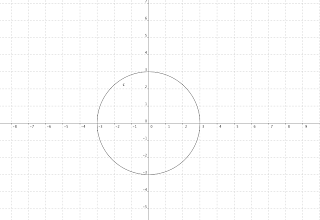
This is an ellipse. Example: x^2 + y^2 = 9
Question 5 of homework 2-solving quadratic equations Tier C
Given that the roots of the equation 2x^2 - 6x - k = 0 differ by 5, find the value of k.
First, we ask ourselves what can be the lowest value of k.
Lowest value of k: 0
So if we input y = 2x^2 - 6x - 0 into Geogebra we will get this (if not through factorisation) :
As we can see, the roots of this equation only differs by 3, not 5.
So we work on the line of symmetry
The parabola can be moved up and down the same line of symmetry.
So we look for the next set of numbers that differ by 5, -1 and 4.
As a result we will get this:
Now the roots differ by 5. Note that they have the same line of symmetry
Now having found the correct parabola that has roots that differ by 5, we should be wondering: how do we put this into an equation.
Well since we just “moved” the parabola, the ax^2 and bx should be the same. Only the c changes.





can you pls write the equation,thx
ReplyDelete