Week 4 learning points

Concepts:
-When moving the parabola up or down, the Line of Symmetry(LoS) remains the same.
-Negative Square Root = NO SOLUTION!
-It is possible for a parabola to have equal roots= 1 root OR 1 line OR never intercept at all which is no solution
-Solving a parabola = finding the point where 2 intercepts Or where it intercepts the x -axis
-Not rational number cannot be solved by factorisation


When completing a square, you are trying to make the equation into (a+b)^2 or (a-b)^2
So for example: x^2+ 2x+ 2=0
x^2 +2x = -2
So, multiply the coefficient of 2x which is 2 so = 4
Then square it so its  4^2
Then add it to the other side to equal the equation out.
Thus,
x^2 + 2x + 4^2 = -5 +4^2
Then solve for x normally.

Learning points in Term 1 Week 2/3

Types of solving equations: 

1. Factorisation

Example: y = x^2 + x - 6 

                Factorise by trial and error    

                You should get y = (x+3)(x+2)

-------------------------------------------------------------------------

However there is another type: what happens when x^2 + x -6 = 0

        The method will be the same as the factorisation 

      Except that the equation will be shown as (x+3)(x-2) = 0

                                                  Therefore if this equation is equivalent to zero, either (x+3) = 0 or (x-2) = 0 as something-zero multiplied by something is zero. 

        Hence, x = -3 OR  x = 2  because if x is 3, (x+3) is 0 and if x is 2, (x-2) = 0.  

1. General formula

y = -(b) ± √ (b)^2 - 4(a)(c) / 2(a)
    

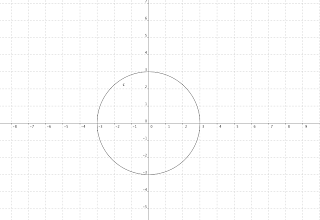
This is an ellipse. Example: x^2 + y^2 = 9

Question 5 of homework 2-solving quadratic equations Tier C

Given that the roots of the equation 2x^2 - 6x - k = 0 differ by 5, find the value of k. 

First, we ask ourselves what can be the lowest value of k. 

Lowest value of k: 0

So if we input y = 2x^2 - 6x - 0 into Geogebra we will get this (if not through factorisation) : 

As we can see, the roots of this equation only differs by 3, not 5. 

So we work on the line of symmetry 

The parabola can be moved up and down the same line of symmetry. 

So we look for the next set of numbers that differ by 5, -1 and 4.

As a result we will get this: 

Now the roots differ by 5. Note that they have the same line of symmetry 

Now having found the correct parabola that has roots that differ by 5, we should be wondering: how do we put this into an equation. 

Well since we just “moved” the parabola, the ax^2 and bx should be the same. Only the c changes. 

Things Learnt In Term 1 Week 2

Monday(10 January 2011)

Ms Loh touched on fractional expressions and she also revised the topic of factorization briefly with us on Monday. The various methods of factorization are shown in the picture below.

Tuesday(11 January 2011)

Today, we covered topics like parabola, subject and algebraic fractions. One of the questions we encountered in the pre-quiz is shown below.

As you can see, we have to factorize the numerator and denominator, such that we can simplify the fraction in a more easier manner. It is encouraged write a statement like "x ≠ -3/2" behind the answer if there is a certain value that does not work on the fraction.

We also encountered another question like this in our pre-quiz. However, this time, we have to make t as the subject of the equation.


Apparently, if the question wants t to be the subject of the equation, the answer should look something like this in the end:

t = ________ (devoid of t; no ts)

We also need to put the "±" sign behind the value, which has been square rooted. This is because the subject of the equation is squared. For example, we can say the value of x squared is 16, so x can be -4 or 4. That is why we must not forget the "±" sign.

This brings us to parabolas. Parabolas have two roots and they are synonymous to the "±" sign. This brings us to a question. Let's say that the equation is y = x^2 and they also stated that y = 4. How can we go about solving this question? We can do this in a graphical perspective like this.


Remember, we have to include the "±" sign behind the square rooted value of 4 as the x, the subject for the current equation, is squared. The picture below shows another approach of solving the same question.


We have to put x, as well as the two other equations given to us, onto the table as shown above. We have to list the numbers out and find similar numbers for the two equations, and not x. After that, we will be able to identify the two differing values of x.

Friday(14 January 2011)

Today, we did some questions of factorization and algebraic fractions. This is one of the questions that we have done in our lesson today.


As you can see, the first step of the solution has two fractions with different denominators. One of them is 3(x - 2), while the other denominator is (x + 3)(x - 2). We have to find the LCM in order to determine the denominator of the algebraic fraction, thus we have to list them out and try to find the desired equation.

(3) (x - 2) (1)
(1) (x - 2) (x + 3)

Since we have to choose the largest number of each column to get the desired LCM, we must determine the denominator, which will be 3(x + 3)(x - 2) in this case. Then, we can proceed and try to solve the algebraic fraction after solving the numerator.

Remember, if the question asks for simplification of the algebraic fraction, do not expand the solution. Otherwise, it is very hard to complete the equation because it is going around in circles. It is also important that we must not forget to write vital steps in our answers, otherwise our marks will be deducted during examinations.

For example, if the question says that y = 2x - 1 and that x = 1, we cannot just answer straightaway. We must have y = 2(1) - 1, before getting 1, which is the answer for the equation.